Using Running Averages in Python to Validate Sensor Data

Handling Signals

If you are writing code to respond to sensor data, you should use a bit of logical abstraction to have clean code that doesn't become harder to work on with time. For example, at a low level, you're getting some signal, likely a voltage, that is supposed to represent another physical signal (in an abstract sense), like a distance or temperature. However, the signal you are actually accessing in the code is just a measurement, e.g. a voltage and not the true distance. At some point in the code, hopefully a well-tested library already written by someone else, this voltage signal has some math done to it and becomes a number that is hopefully pretty close to the measurement we care about. Later on in the code, in regions we are usually responsible for, it would be nice to treat that number as the real thing, and make whatever system we're designing to respond accordingly. Going in blindly, though, can be a recipe for disaster. Why?

Trust, But Verify

Sometimes physical components fail. Maybe someone's skin oil, left behind during setup or installation, is changing some overall resistance and invaliding our assumptions, and math, about a voltage signal across a wire. Water, rust, rot, and an infinite number of other failure mechanisms can plague the best-designed system, so a good rule of thumb is to trust, but verify.

In Python, one way to do this is by using a rolling average, where only measurements in a certain range are included. In a sense, this is a sort of integral control mechanism where our controller output at \(t\) seconds would look something like

\[ u(t) = \frac{K_i(t)}{n} \int_{t-n\ell}^{t} e(\tau)\, \mathrm{d}\tau \]

where we have:

• \(n\) items in the rolling average
• a polling time of \(\ell\) seconds (e.g., each iteration of a while True control loop takes \(\ell\) seconds between measurements)
• a gain/transfer function of \(K_i(t)\), e.g. the scaling factor between a rolling average distance signal input and motor power signal output

However, since we are polling at discrete times, we are taking a sort of Riemann sum approximation, where an increase in the number of rectangles in the approximation can give better performance at the cost of slower response time (this is where an additional derivative control term would help.) Here's an illustration of the error for a simple case where \(e(t) = t^2\) and \(n = 4\).

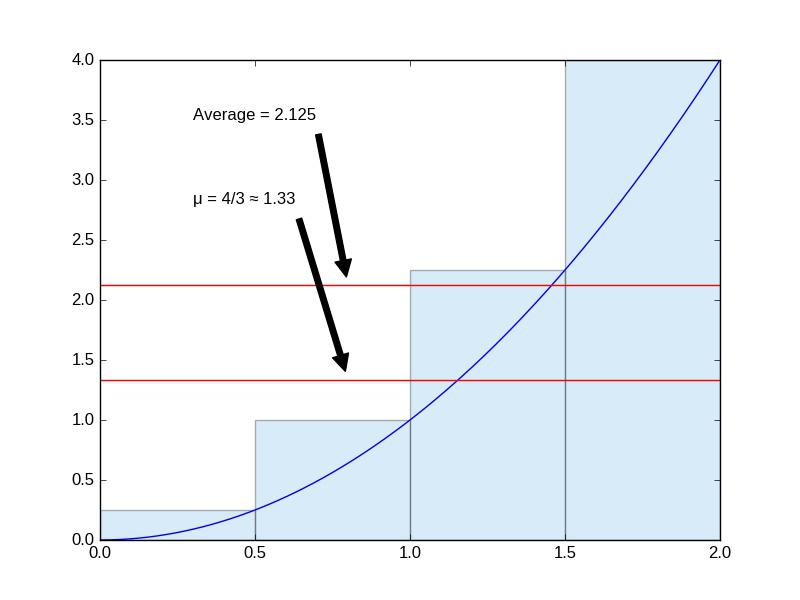
So what's the takeaway?

• We can implement a rolling average to deal with a noisy measurement
• While we're at it, we can include a reasonable upper and lower bound to validate measurements before adding to the rolling average
• The downside is a lag time in response to changes in the measurement, and the lag time goes up with accuracy

Now, on to the code!

# Create empty list-type variable so we can
# store measurements
sensor_measurements = []

# Declare these variables at a top level so you can
# easily edit them once for your whole script to
# test performance
upper_reasonable_bound = 200
lower_reasonable_bound = 0
rolling_average_size = 4

def average(measurements):
  """
  Use the builtin functions sum and len to make a quick average function
  """
  # Handle division by zero error
  if len(measurements) != 0:
    return sum(measurements)/len(measurements)
  else:
    # When you use the average later, make sure to include something like
    # sensor_average = rolling_average(sensor_measurements)
    # if (conditions) and sensor_average > -1:
    # This way, -1 can be used as an "invalid" value
    return -1

def rolling_average(measurement, measurements):
  # Update rolling average if measurement is ok, otherwise
  # skip to returning the average from previous values
  if lower_reasonable_bound < measurement < upper_reasonable_bound:
    # Remove first item from list if it's full according to our chosen size
    if len(measurements) >= rolling_average_size:
      measurements.pop(0)
    measurements.append(measurement)
  return average(measurements)

# Your control loop may be handled in another file
# or with another method, here's an example usage
import some_sensor_module as ssm
while True:
  sensor_measurement = ssm.some_sensor_function()
  sensor_value = rolling_average(sensor_measurement, sensor_measurements)
  if (condition_using_sensor_value) and sensor_value > -1:
    some_logic_handler_function(sensor_value)
  else:
    # and so forth

Let me know in the comments if you have any questions or feedback!